如果这篇博客帮助到你,可以请我喝一杯咖啡~
CC BY 4.0 (除特别声明或转载文章外)
一 STL 组成
graph LR
A[STL] --- B[容器 container]
A --- C[配接器 adapter]
A --- D[迭代器 iterator]
A --- E[仿函数 function]
A --- F[算法 algorithm]
A --- G[空间配置器 allocator]
二 常用容器
.png)
容器简介
下面我们来简单看一下这些容器的常用接口的使用,并分析其复杂度
vector
.png)
list
.png)
deque
.png)
stack
.png)
queue
.png)
priority_queue
.png)
set & multiset
.png)
map & multimap
.png)
unordered_map & unordered_multimap
| unordered_map | |
|---|---|
| 底层实现: | 动态数组 + 链表(红黑树) |
| 查找: | find() |
| 计数: | count() |
| 指定插入: | insert() |
| 指定删除: | erase() |
| 随机访问 | operator[] |
由于底层实现哈希表的时候,会有负载因子的存在,所以可以认为上述操作的复杂度都为 O(1)
如果哈希冲突比较多,可以采用 动态数组 + 红黑树实现,复杂度最多为 O(logn)
因此,哈希表的优势为 O(1) 的查找;这是一种以空间换时间的策略。
容器选择
不知道使用什么容器时,优先选择
vector如果不需要频繁的任意位置插入,需要支持随机访问,选择
vector如果不需要随机访问,需要频繁的插入,选择
list如果需要频繁的对头/尾操作,选择
deque如果需要高效的查找,但对内存没有限制,可以选择
unordered_map;如果对内存有限制,可以选择set/mapdeque在 STL 中作为stack和queue底层实现。其优势为:- 相比于
vector:头部插入和删除以及扩容时,效率更高,因为不需要搬大量的元素 - 相比于
list:底层空间更为连续,空间利用率更高
劣势为:不适合遍历,因为在遍历时,
deque的迭代器要频繁的去检测其是否移动到某段小空间的边界,导致效率低下- 相比于
三 迭代器
1. 迭代器种类
迭代器种类一节摘自: Stl整理
C++中,一图解释五类迭代器之间的继承关系:
graph LR
A[输入迭代器]
B[输出迭代器]
C[前向迭代器]
D[双向迭代器]
E[随机访问迭代器]
A --> C
B --> C
C --> D
D --> E
输入迭代器(input iterator)
只读,不写;单遍扫描,只能递增。
输入迭代器只支持顺序访问,通常用于读取序列中的元素。对于一个输入迭代器it,*it++保证是有效的,但递增它可能导致所有其他指向流的迭代器失效。其结果就是,不保证其状态可以保存下来并用来访问元素。因此,输入迭代器只能用于单遍扫描的算法。支持如下操作:
- 相等(
==)、不等(!=)比较。 - 用于推进迭代器的前置和后置递增(
++)。 - 解引用(
*),只能出现在赋值运算的右侧;箭头运算符(->),it->member等价于(*it).member。
算法find要求输入迭代器;而类型istream_iterator是一种输入迭代器。
输出迭代器(output iterator)
只写,不读;单遍扫描,只能递增。可以看作输入迭代器功能上的补集。
只能向解引用的输出迭代器赋值一次,类似输入迭代器,输出迭代器也只能用于单遍扫描的算法,通常用作算法的目标位置。支持如下操作:
- 用于推进迭代器的前置和后置递增(
++)。 - 解引用(
*),只能出现在赋值运算的左侧。
算法fill要求输出迭代器;而类型ostream_iterator是一种输出迭代器。
前向迭代器(forward iterator)
可读写;多遍扫描,只能递增。
可以读写元素,只能在序列中沿着一个方向移动,支持所有输入迭代器和输出迭代器的操作,而且可以多次读写同一个元素。因此,可以保存前向迭代器的状态,使用前向迭代器的算法可以进行多遍扫描。
算法replace要求前向迭代器;容器forward_list上的迭代器是前向迭代器。
双向迭代器(bidrectional iterator)
可读写;多遍扫描,能递增递减。
可正向/反向读写序列中的元素。除支持所有前向迭代器的操作之外,双向迭代器还支持前置和后置递减(--)。
算法reverse要求双向迭代器;除了forward_list之外,其他标准库容器上的迭代器都是双向迭代器。
随机访问迭代器(random-access iterator)
可读写;多遍扫描,支持全部迭代器运算。
提供在常数时间内访问序列中任意元素的能力,除支持双向迭代器的所有操作外,还支持:
- 用于比较两个迭代器的相对位置(
>、<、>=、<=)。 - 迭代器和一个整数值的加减运算(
+、+=、-、-=),计算结果迭代器在序列中前进或后退给定整数后的迭代器。 - 迭代器之间的减法(
-),得到两个迭代器之间的距离。 - 下标运算符(
[]),it[n]与*(it+n)等价。
算法sort要求随机访问迭代器;容器vector上的迭代器和用于访问内置数组的指针是随机访问迭代器。
2. 迭代器失效
图片来源 cppreference
.png)
3. 迭代器实现
以下都是迭代器的简单实现,要看对容器的完整实现,请去我的 Github,链接如下:
https://github.com/hairrrrr/Cpp-Primer
记得留下你的 star 哟~
deque
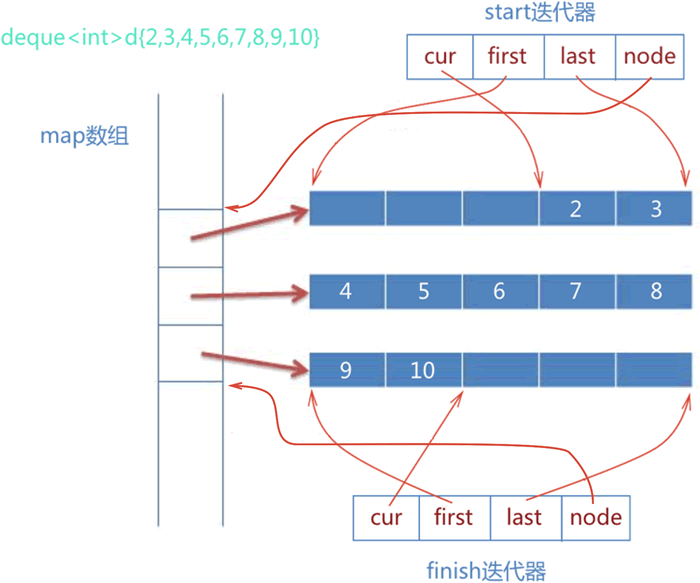
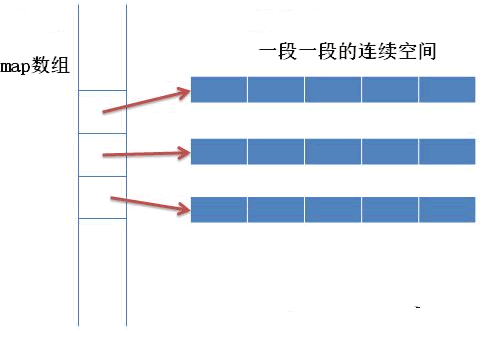
简单实现:
template<class T,...>
struct __deque_iterator{
...
T* cur;
T* first;
T* last;
map_pointer node;//map_pointer 等价于 T**
}
//当迭代器处于当前连续空间边缘的位置时,如果继续遍历,就需要跳跃到其它的连续空间中,该函数可用来实现此功能
void set_node(map_pointer new_node){
node = new_node;//记录新的连续空间在 map 数组中的位置
first = *new_node; //更新 first 指针
//更新 last 指针,difference_type(buffer_size())表示每段连续空间的长度
last = first + difference_type(buffer_size());
}
//重载 * 运算符
reference operator*() const{return *cur;}
pointer operator->() const{return &(operator *());}
//重载前置 ++ 运算符
self & operator++(){
++cur;
//处理 cur 处于连续空间边缘的特殊情况
if(cur == last){
//调用该函数,将迭代器跳跃到下一个连续空间中
set_node(node+1);
//对 cur 重新赋值
cur = first;
}
return *this;
}
//重置前置 -- 运算符
self& operator--(){
//如果 cur 位于连续空间边缘,则先将迭代器跳跃到前一个连续空间中
if(cur == first){
set_node(node-1);
cur == last;
}
--cur;
return *this;
}
list
/**
* ListNode: 链表的节点类型
*/
template<class T>
struct ListNode
{
T _value;
ListNode* _next;
ListNode* _prev;
ListNode(const T& val = T())
:_value(val)
,_next(nullptr)
,_prev(nullptr)
{}
};
/**
* ListIterator: 链表的迭代器
* 类类型的迭代器不是指针,而是一个类。
* 各种操作其实本质是操作 ListNode 中的某个成员
*/
template<class T, class Ref, class Ptr>
struct ListIterator
{
typedef ListNode<T> Node;
typedef ListIterator<T, Ref, Ptr> Self;
ListIterator(Node* node)
:_node(node)
{}
Ref operator*()
{
return _node->_value;
}
/**
* -> 当作单目运算符处理
* 类类型中的元素访问模式:ListNode->_val->某一个元素
* 中间的 ->_val 被编译器优化
*/
Ptr operator->()
{
return &_node->_value;
}
Self& operator++()
{
_node = _node->_next;
return *this;
}
Self& operator--()
{
_node = _node->_prev;
return *this;
}
bool operator!=(const Self& it)
{
return _node != it._node;
}
Node* _node;
};
因为 map & set & multimap & multiset 底层都是用红黑树实现的,因此,我们有必要看一下红黑树的迭代器如何实现。
红黑树
template<class Value>
struct RBNode
{
typedef RBNode<Value>* Ptr_RBNode;
Value _data;
Color _color;
Ptr_RBNode _left;
Ptr_RBNode _right;
Ptr_RBNode _parent;
RBNode(const Value& data = Value())
:_data(data)
,_color(RED) // 节点颜色默认初始化为 red
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
{}
};
template<class Value>
struct RBIterator
{
typedef RBNode<Value> Node;
typedef RBIterator Self;
Node* _node;
RBIterator(Node* node)
:_node(node)
{}
Value& operator*()
{
return _node->_data;
}
Value* operator->()
{
return &_node->_data;
}
bool operator==(const Self& it)
{
return _node == it._node;
}
bool operator!=(const Self& it)
{
return _node != it._node;
}
Self& operator++()
{
// 如果当前节点有右节点
if (_node->_right)
{
_node = _node->_right;
// 让 _node 设为最右节点
while (_node->_left)
_node = _node->_left;
}
// 向上回溯,如果当前节点为父节点的右节点,继续向上回溯
else
{
Node* parent = _node->_parent;
while (_node == parent->_right)
{
_node = parent;
parent = parent->_parent;
}
// 当 parent 为 _header ,_node 为整个树的根节点时,
// 一定会退出上面的 while 循环,此时应该将 _node 置为 _header
// 如果 _node 不在父节点的左侧,也应该单独执行一次,将 _node 指向下一次访问的节点
/*_node = parent;*/
// 上面的写法有一个问题,如果整个树只有一个节点。_header->right == _node
// _node 会走到 _header, parent 走到 _node 此时退出循环
// _node 再被赋值为 _node , 所以迭代器的遍历会陷入循环
if (_node->_right != parent)
_node = parent;
}
return *this;
}
};
map 和 set 的迭代器只是对红黑树的迭代器进行了封装,然后给出了 begin() 和 end() 方法。
哈希表
template<class K, class V, class keyOfValue, class HashFun>
struct HashIterator
{
typedef HashNode<V> Node;
typedef HashTable<K, V, keyOfValue, HashFun> _HashTable;
typedef HashIterator<K, V, keyOfValue, HashFun> Self;
Node* _node;
_HashTable* _ht;
HashIterator( Node* node, _HashTable* ht)
:_node(node)
,_ht(ht)
{}
V& operator*() const
{
return _node->_value;
}
V* operator->() const
{
return &_node->_value;
}
bool operator!=(const Self& it) const
{
return _node != it._node;
}
Self& operator++()
{
// 如果 _node._next 存在
if (_node->_next != nullptr)
{
_node = _node->_next;
}
// 在哈希表中向后寻找非空链表
else
{
keyOfValue kov;
HashFun hf;
int idx = hf(kov(_node->_value)) % _ht->_table.size();
idx++;
for (; idx < _ht->_table.size(); idx++)
{
if (_ht->_table[idx])
{
_node = _ht->_table[idx];
break;
}
}
// 哈希表已遍历完
if (idx == _ht->_table.size())
_node = nullptr;
return *this;
}
}
};
四 仿函数
priority_queue 默认是一个“大根堆”,使用如下代码测试:
int main(void)
{
priority_queue<int> pq;
pq.push(9);
pq.push(5);
pq.push(2);
pq.push(7);
while (!pq.empty())
{
cout << pq.top() << endl;
pq.pop();
}
}
输出:
9
7
5
2
如果我们想要堆中最小的元素,也就是建立一个“小根堆”,可以通过这种方式定义 pq:
priority_queue<int, vector<int>, greater<int>> pq;
第二个参数表示 priority_queue 内部的实现方式,第三个参数定义了比较规则
我们也可以自己来定义比较规则:
template<class T>
struct MyGreater : public binary_function<T, T, bool>
{
bool operator()(const T& lhs, const T& rhs)
{
return lhs > rhs;
}
};
然后通过如下方式调用:
priority_queue<int, vector<int>, MyGreater<int>> pq;
五 空间配置器
未完待续。。。
六 算法
未完待续。。。
参考文章:
C++ 学习代码仓库:https://github.com/hairrrrr/Cpp-Primer
C 语言学习代码仓库:https://github.com/hairrrrr/C-CrashCourse
